사소해 보이는 연산 뒤에 숨어있는 것

이 글은 대학원 시절, 대략 2010년 정도에 인턴 전화 면접을 하면서 겪은 인상 깊었던 일에 관한 것이다. 요즘은 기가 막힌 온라인 코딩 테스팅 서비스가 여럿 있지만, 당시는 그냥 구글 닥스 같은 곳에서 구문 강조도 없이 코딩했다. 그 전화 면접에서 받았던 문제는 이러했다.

“이진 탐색 트리(BST, binary search tree)에서 중위(in-order) 순회를 하는 반복자(iterator)를 구현하고 싶어요. 반복자를 만드는데 필요한 begin과 next 함수를 만들어 보세요.”

학부 알고리즘 수업을 들은 지 얼마 안 된 분이라면 금방 풀 수도 있다. 그런데 시간이 좀 지났다면 직접 트리 그려가면서 알고리즘을 찾아야 한다. 긴장하면 삽질하기 쉬운 문제이기도 하다.

이진 탐색 트리에서 중위 순회는 트리에 담긴 값을 정렬된 순서로 탐색하는 것과 같다. 결국, begin 함수는 트리의 최솟값¹을 찾는 것이며, next는 주어진 노드의 바로 다음 노드를 찾는 것이다. 최솟값은 트리의 제일 왼쪽 끝에 있으므로 간단하게 구현된다. 그런데 next처럼 주어진 노드의 다음 노드(successor)를 찾는 건 경우의 수를 따져야 한다. CLRS 알고리즘 책에 있는 트리 그림(Figure 12.2)으로 생각해보자.

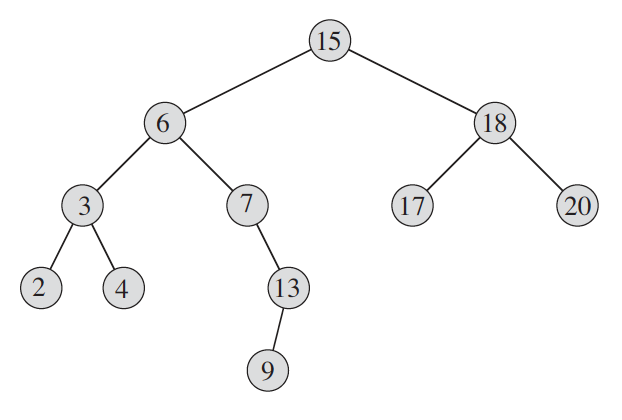
주어진 노드가 루트인 15라고 하자. 15의 다음 노드는 17인데, 가만히 보면 오른쪽 자식 서브 트리의 최솟값임을 확인할 수 있다. 즉, 만약 주어진 노드에 오른쪽 자식이 있으면, 오른쪽 서브 트리의 최솟값을 구하면 된다. 간단하다.

이제 오른쪽 자식이 없는 경우를 생각하자. 실수를 막으려면 약간 복잡한 트리를 놓고 추론해야 한다. 위 그림에서 노드 13을 보자. 13의 다음 노드는 15이다. 어떻게 15까지 찾아갈 수 있을까? 각 노드에 부모 정보가 없다면 더 어려운 문제가 되는데 부모 포인터는 있다고 생각하자. 나는 이렇게 답했다. (뒤에서 곧 밝혀지겠지만 여기에 사소한 실수가 있었다.)

“부모를 루트까지 쭉 타고 올라가면서 자신의 값보다 작지 않은 첫 번째 부모를 선택하면 되겠네요.”

맞는 것 같아서 이렇게 코드를 만들었다.

1
2
3
4
5
6
7
8
9
10
11
Node* next(Node* node) {
  if (node == NULL) return NULL;
  if (node->right != NULL) {
    return findMinimum(node->right);
  } else {
      Node* parent = node->parent;
      while (parent != NULL && parent->value < node->value)
        parent = parent->parent;
      return parent;
  }
}

요즘은 직접 온라인 컴파일러까지 되므로 바로 테스트 케이스도 돌려볼 수 있지만, 당시는 한 줄씩 검산했었다. 인터뷰어가 잘했다고 말하면서 하나를 지적했다.

“틀린 것은 아닌데, 하나 고쳐야 할 부분이 있어요. 보이나요?”

내가 좀 당황하자 인터뷰어가 위치를 가르쳐줬다.

“부모의 값과 비교할 때 < 연산자가 있죠? (라인 7) 무슨 문제가 있을까요?”

그제야 무얼 말하는지 알았다.

지금 예에서는 노드 값 타입이 정수이므로 비교 연산이 CPU에서 가장 빠른 연산 중 하나이다. 그런데 만약 노드 값이 아주 복잡하고 큰 자료라서 비교 연산에 시간이 오래 걸린다면? 얼마든지 있을 수 있는 일이다. 트리에 노드를 추가/삭제할 때는 반드시 이 비교 연산을 해야 한다. 하지만 단순히 순회하는데 시간이 오래 걸릴 수 있는 비교 연산을 수행하는 것은 옳지 않다. 다행히 답을 할 수 있었다.

“그렇다면 어떻게 고치면 될까요?”

잘 안 보여서 다시 약간의 삽질 끝에 드디어 답을 찾아냈다. 값을 비교하는 것이 아니라 내가 부모의 왼쪽 또는 오른쪽 자식인지 확인하면 되는 것이다. 이건 단순히 노드 포인터 - 포인터가 없는 언어라도 - 비교에 지나지 않으므로 32비트 혹은 64비트 정수 비교 연산과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Node* next(Node* node) {
  if (node == NULL) return NULL;
  if (node->right != NULL) {
    return findMinimum(node->right);
  } else {
      Node* parent = node->parent;
      while (parent != NULL && parent->right == node) {
      //                       ~~~~~~~~~~~~~~~~~~~~~
        node = parent;
        parent = parent->parent;
      }
      return parent;
  }
}

뒤늦게 CLSR 교과서에 소개된 알고리즘을 봐도 < 연산이 아닌 오른쪽 자식이냐로 판별하고 있다. LLVM C++ 라이브러리인 libc++의 구현을 봐도 그러하다.

사소해 보이는 < 연산에 큰 대가가 숨어있을 수 있음을 깨닫게 해준 아주 기억에 남는 인터뷰였다. (음, 연산자 오버로딩을 탓할 수도 있겠다.) 이 이야기는 저수준에서 코드를 다뤄야 하는 C/C++ 프로그래머에게만 적용되는 이야기는 아니다. 파이썬이던 자바스크립트이던 프로그래머는 시간만 허락한다면 효율적인 코드를 만들어야 한다.

그때 교훈으로 지금도 내가 숨어있는 것도 볼 수 있는 프로그래머인지 반문한다.